Advent of Code 2024 [Writeup]
Dec 2024
The following are writeups for each day's puzzles of advent of code 2024. All solutions are written in Python and can be found here https://github.com/hexhowells/AdventOfCode. My writeups for last years advent of code can be found here https://hexhowells.com/posts/aoc-2023.html
- Day 01
- Day 02
- Day 03
- Day 04
- Day 05
- Day 06
- Day 07
- Day 08
- Day 09
- Day 10
- Day 11
- Day 12
- Day 13
- Day 14
- Day 15
- Day 16
- Day 17
- Day 18
- Day 19
- Day 20
- Day 21
- Day 22
- Day 23
- Day 24
- Day 25
Day 01
Puzzle · SolutionPart 1
Each line consists of 2 integers separated by some spaces. We need to extract each pair of integers from the list into two separate lists, sort them, then sum the differences of each pair. This is done with the following code:
def part1(x):
l1, l2 = [], []
for line in x:
a, b = line.split()
l1.append(int(a))
l2.append(int(b))
l1 = sorted(l1)
l2 = sorted(l2)
return sum([abs(a - b) for a, b in zip(l1, l2)])
Part 2
Part 2 requires us to iterate over each element of the first list and sum together the product of its value and its count in the second list. If it doesn't appear in the second list we can still perform the operation since its count will be 0 and will 0 the multiply operation. The code for part 2 is below:
def part2(x):
l1, l2 = [], []
for line in x:
a, b = line.split()
l1.append(int(a))
l2.append(int(b))
return sum([l * l2.count(l) for l in l1])
Day 02
Puzzle · SolutionPart 1
In the first part we need to check if each line is either increasing or decreasing and that each difference between each pair of numbers are between 1 and 3. This can be done by checking if each line is equal to the line sorted in either increasing or decreasing order. Checking for differences is pretty straight forward. The following condensed function performs this check:
def safe(n):
if (n == sorted(n)) or (n == sorted(n, reverse=True)):
return sum( [not(0 < abs(a - b) <= 3) for a, b, in zip(n, n[1:])] ) == 0
else:
return False
Part 2
Part 2 includes the checking/counting of the first part. However, now if each line doesn't pass the safety check, we need to also check if removing any single integer will cause the pass to check. We can write an additional function to iterate over each subarray where each integer is removed and checked for safety:
def check(n):
good = 0
for i in range(len(n)):
good += safe(n[:i] + n[i+1:])
return good
Day 03
Puzzle · SolutionPart 1
Both parts of today's puzzle can be solved pretty easy by using regex to extract out the instructions from the corrupted program. Processing the instructions then requires parsing out the integers, multiplying, then summing to get the answer. We can use the following regex to extract out the mul instructions:
mul\(\d+,\d+\)
Part 2
Part 2 can be solved by extending out our regex to also extract do() and don't() instructions. We then just maintain a flag containing the state of whether to execute the mul instructions. We can use the following regex to extract all of the instructions needed in part 2:
mul\(\d+,\d+\)|don't\(\)|do\(\)
Day 04
Puzzle · SolutionPart 1
For each point on the grid, search out in each direction for the string XMAS. For each match found increment a global counter keeping track of the total number of occurrences of the word. Since I have a custom grid class for handling grids this isn't too difficult.
Part 2
For part 2, I iterated through each point and assumed it was the center of the X. Then find the 4 corners of the X and check each diagonal for either permutation of M and S. If the center contains an A and both diagonals contain M and S then increment a global counter.
Day 05
Puzzle · SolutionPart 1
For today's problem, we need to verify that each page in the list is valid according to a list of rules. The rules state that value A must come after value B. This can also be written as value B cannot come before value A. This can be checked by iterating through the elements in the page, and for each element x no values before x appear in a rule involving x as the prior.
So looking at the sequence 75,97,47,61,53, the page is invalid as the rule 97|75 implies that 75 must come after 97.
Programmatically, this can be checked by creating a set of all the rules as strings, and for every pair of values, creating a fake rule that would invalidate the page. If that rule actually exists in the rule set, then we know the page is invalid. So for the pair 75,97 in the sequence, we can create the fake rule 97|75, which, if this rule exists in the rule set, would mean this page is invalid.
From here, we then check each page and sum the middle value of all pages that are valid.
The code for this checking function is below, rules is a set of all the rule strings.
def valid(p, rules):
for i in range(1, len(p)):
for j in range(i):
if f'{p[i]}|{p[j]}' in rules: return False
return True
Part 2
Part 2 is pretty simple if we leverage the solution to part 1. Here we can use the same code to check any invalid pairs. If a pair of values (A, B) is invalid, we simply move value B to the left of value A. We do these check and fix operations for each pair of values in the page to fix it (if its invalid). For every page that required fixing, we sum the middle value of the sequence to derive the answer.
The following is essentially the same code as above but fixes the page instead of flagging whether the page is valid or not.
def fix(p, rules):
for i in range(1, len(p)):
for j in range(i):
if f'{p[i]}|{p[j]}' in rules:
p.insert(j, p.pop(i))
return p
Day 06
Puzzle · SolutionPart 1
In order to traverse the grid we need to keep track of the current position and direction of the guard. We then calculate the next position based on the current direction. If the next position is an obstruction then we rotate the direction, if the next position if off the grid then we halt, otherwise we update our current position to the next position.
Every movement the guard makes, we maintain the position in a set, returning the length of the set after reaching the edge of the grid gives us our answer!
Part 2
Part 2 can be done with brute force and some pruning of the search space. The first thing to recognise is that the path of the guard will only be effected if an obstacle is placed somewhere on the original path. If an obstacle is placed anywhere else then the guard will never interact with it.
No obstacle placed at a '.' will effect the following path:
...#......
....>>>>v#
....^...v.
..#.^...v.
..>>^>v#v.
..^.^.v.v.
.#^<^<<<<.
.>>>>>vv#.
#^<<<<<v..
......#v..
So for every position on the grid that is apart of the original path (excluding the starting position), we can place an obstacle and check for loops.
We check for loops by following the new path and keeping track of all the positions and directions we have been in. If at any point we end up in a position and direction that we've already seen before, then we're in a loop. Otherwise we will eventually terminate at the edge of the grid. Counting all the positions where a loop occurs if we place a new obstacle gives us the answer to part 2!
Day 07
Puzzle · SolutionPart 1
Part 1 can be solved using brute force by iterating over each possible combination of operators. Operators can be defined using lambda functions and all possible combinations can be created using itertools.combinations over the lambda functions.
add = lambda a, b: a + b
mul = lambda a, b: a * b
Part 2
Part 2 can be solved via the same method of brute force but adding in a pipe operator.
pipe = lambda a, b: int(str(a) + str(b))
A slight optimisation is to compute part 1 and 2 together. Checking for combinations of the + and * symbols first, then only if that isn't valid, checking with the || operator for part 2. The solution described runs in about 30 seconds.
for test_value, ops in input_data:
if check(test_value, ops, [add, mul]):
p1 += test_value
p2 += test_value
elif check(test_value, ops, [add, mul, pipe]):
p2 += test_value
To further improve this solution, we can iterate over all possible combinations using recursion. Here we can recursively check each combination of operators starting from left to right. Since the operators accumulate the values from left to right, recursion maintains the accumulator so it doesn't get re-computed for each possible combination.
In the below example, a + b and a * b are computed twice using a pure brute force approach where expressions are fully evaluated each time.
a + b + c
a + b * c
a * b + c
a * b * c
But using recursion we compute the first pair of values with a given operator, then given that value as the accumulator, recursively check each possible operator for the accumulator and the next value. Thus we only had to compute the first pair of values once for a given operator. This optimisation holds true for each accumulated pair of values at each depth in the recursion.
checking a + b
+ c
* c
checking a * b
+ c
* c
Day 08
Puzzle · SolutionPart 1
In order to find antinodes that are in line with a pair of transmitters, we can get the x, y difference between the two transmitters and add them to both transmitter coordinates. Take the following grid with two transmitters (assume they have matching symbols):
..........
..........
..........
....a.....
..........
.....b....
..........
..........
..........
..........
a = (3, 4)
b = (5, 5)
Getting the row/column difference between each point:
..........
..........
..........
....a-....
.....|....
.....b....
..........
..........
..........
..........
row difference between a and b = -2
column difference between a and b = -1
row difference between b and a = 2
column difference between b and a = 1
With the two different row/column differences, we can add them to their respective transmitter:
adding a to diff
a = (3, 4) + (-2, -1) = (1, 3)
..........
...#......
..........
....a-....
.....|....
.....b....
..........
..........
..........
..........
adding b to diff
b = (5, 5) + (2, 1) = (7, 6)
..........
...#......
..........
....a-....
.....|....
.....b....
..........
......#...
..........
..........
For every pair of matching transmitters, we find all antinodes. Then, for every antinode we find, we keep track of its coordinates in a set. The length of the set at the end is the answer to part 1.
Part 2
Part 2 uses the same logic as part 1 but for every antinode found, we continue to increment its coordinates with the transmitter difference. Given our example above and the 2 antinodes found:
adding a antinode to diff
#(a) = (1, 3) + (-2, -1) = (-1, 2)
!
..........
...#......
..........
....a-....
.....|....
.....b....
..........
......#...
..........
..........
Invalid antinode! Outside of grid.
adding b antinode to diff
#(b) = (7, 6) + (2, 1) = (9, 7)
..........
...#......
..........
....a-....
.....|....
.....b....
..........
......#...
..........
.......#..
Then continuing from the node found
adding new b antinode to diff
#(b) = (9, 7) + (2, 1) = (11, 8)
..........
...#......
..........
....a-....
.....|....
.....b....
..........
......#...
..........
.......#..
!
Invalid antinode! Outside of grid.
After performing this search, we can do the same as part 1, keeping track of all the antinode coordinates and summing the total count. A key thing to node is that the two transmitters always count towards an antinode, since they are in line with the pair at equal distances.
Day 09
Puzzle · SolutionPart 1
In part 1 we can expand out the disk map into blocks. We can then solve this part using the two-pointer technique. Here we maintain two pointers at either end of the array of blocks. The left pointer increments along the array, if it encounters an empty block (.), then we decrement the right pointer until we reach a file block, we then swap the two values. We continue doing this until the two pointers meet, at which point we have moved all the files back.
We can then compute the checksum by following the rules in the puzzle.
Part 2
Part 2 is more tricky since we have to move entire files consisting of multiple blocks. Thus instead of expanding out the disk map, we instead maintain a tuple consisting of the file ID (of blank space) and how many blocks it's made up of. So the following expanded disk map:
0..111....22222
Will look like the following:
(0, 1), ('.', 2), (1, 3), ('.', 4), (2, 5)
Then going from right to left, we try to move the file into an available empty space. This is done by checking the filesize (in blocks) and comparing to each empty space left to right. If we encounter an empty space that can fit the file, there are two possible outcomes:
- The number of blocks in the file and empty space match, so we move the file into where the empty space was and replace the original file location with an empty space id
'.' - The file size has less blocks in the empty space, so there will be space remaining. In which case we still replace the empty space with the file and replace the original file's ID with an empty space. But we also insert a new empty space file consisting of the
number of blocks in the empty space-the number of blocks in the file
The following show an example of moving a file with the same space:
Moving file (2, 5)
(0, 1), ('.', 2), (1, 3), ('.', 4), (2, 2)
^
not empty
(0, 1), ('.', 2), (1, 3), ('.', 4), (2, 2)
^
empty! moving...
(0, 1), (2, 2), (1, 3), ('.', 4), ('.', 2)
| |
L------ swap symbols ------⅃
The following show an example of moving a file with space remaining:
Moving file (2, 5)
(0, 1), ('.', 5), (1, 3), ('.', 4), (2, 2)
^
not empty
(0, 1), ('.', 5), (1, 3), ('.', 4), (2, 2)
^
empty! moving...
Γ---<--- move chunks ---<---⅂
v ^
(0, 1), (2, 2), (1, 3), ('.', 4), ('.', 2)
| |
L------ swap symbols ------⅃
Remaining empty chunks
5 - 2 = 3
Insert empty chunks after file
(0, 1), (2, 2), ('.', 5), (1, 3), ('.', 4), ('.', 2)
^
insert empty chunks
Once we have gone through the entire list of blocks, we can follow the same rules in part 1 to compute the checksum
Day 10
Puzzle · SolutionPart 1
Part 1 can be solved with a search algorithm such as breadth-first search or depth-first search. Where the termination statement is encountering a 9 and we only search neighbours that have an increment of 1. The following function implements this using a custom grid function:
def BFS(grid, start):
seen = set()
q = deque([start])
count = 0
while q:
node = q.popleft()
if node not in seen:
seen.add(node)
if grid.get(node) == 9: count += 1
q.extend([n for n in grid.get_neighbour_coords(node) if (grid.get(n) - grid.get(node) == 1)])
return count
Part 2
Part 2 has the same solution as part 1 except we visit nodes we have already visited. So we simply remove the seen variable and conditional.
Day 11
Puzzle · SolutionPart 1
Part 1 can be solved pretty easily by computing the rules for each number, for 25 iterations.
Part 2
For 75 iterations, computing the raw array of numbers becomes infeasible due to exponential growth. Instead we can compute the number of stones using recursion and dynamic programming. Meaning we don't have to store a huge list of numbers. Consider the evolution of a single number as a tree:
depth 0: 125
|
depth 1: 253000
/ \
depth 2: 253 0
| |
depth 3: 512072 1
/ \ |
depth 4: 512 72 2024
For any given node on the tree, we can compute how many times it branches (until reaching the given depth), this information can be propagated up the tree to the root node. So we can write a function to recursively go down each branch and compute how many times it's children branch before hitting the depth limit. The following code gives our recursive function:
def blink(stone, depth, lim):
if depth == lim:
return 1
if stone == 0:
return blink(1, depth+1, lim)
elif len(str(stone)) % 2 == 0:
stone_str = str(stone)
split = len(stone_str) // 2
left_half = int(stone_str[:split])
right_half = int(stone_str[split:])
return blink(left_half, depth+1, lim) + blink(right_half, depth+1, lim)
else:
return blink((stone * 2024), depth+1, lim)
So if each rule never led to a split stone, then at the terminal node, a 1 would be returned, which would propagate up each parent node until it got to the root. Whenever there is a split, we explore both children and sum their branch counts.
This solution is still going to be too slow though. So to speed things up more we can use dynamic programming using memoization to cache the results of each function call. This works since the results of exploring a given node are deterministic. Thus, looking at our example tree above, the number of branches after the node 253 is 2. So now next time we encounter a node with the value 253 we don't need to explore any more children and can just use our cached answer.
This can be done to the above function using the function decorator @cache from the functools standard library. This will cache the result for any given input. Applying memoization to our function will enable it to run in less than a second and give us the answer to part 2!
Day 12
Puzzle · SolutionPart 1
We can get the coordinates of each garden plot via the flood fill algorithm. By iterating over each point, and if that point wasn't already found with flood fill (that plot has already been found), then use flood fill to get all the point of that plot.
To compute the perimeter, we iterate over each point in the plot, and count all the edges that don't touch another point in the plot. The sum of the edges for each point in the plot is the perimeter.
Part 2
For part 2 instead of trying to find the number of sides of each plot by looking at the points or border, we can instead brute force through all the horizontal and vertical edge pairs. Consider the following:
AAAAAA
AAABBA
AAABBA
ABBAAA
ABBAAA
AAAAAA
We can iterate over each pair of vertical edges by iterating over each pair of rows:
Checking first pair of columns
A <-> AAAAA
A <-> AABBA
A <-> AABBA
A <-> BBAAA
A <-> BBAAA
A <-> AAAAA
For each pair of points in the columns, we check if one of the points belong to a given plot (so the edge is bordering the plot). If the edge is bordering the plot then we have found an edge! To search for continuous edges, we need to keep track of whether the last edge pair was part of the plots edge.
Checking edges for plot A
Checking first pair of columns
A <-> AAAAA
A <-> AABBA
A <-> AABBA
A <-> BBAAA
A <-> BBAAA
A <-> AAAAA
A <-> AAAAA <- (A, A) edge contains two A's, so no edge found
A <-> AABBA
A <-> AABBA
A <-> BBAAA
A <-> BBAAA
A <-> AAAAA
...
A <-> AAAAA
A <-> AABBA
A <-> AABBA
A <-> BBAAA <- (A, B) edge pairs contain one A, found edge!
A <-> BBAAA
A <-> AAAAA
A <-> AAAAA
A <-> AABBA
A <-> AABBA
A <-> BBAAA
A <-> BBAAA <- (A, B) edge pairs contain one A, but so did
A <-> AAAAA previous edge pair, so no new edge found
A <-> AAAAA
A <-> AABBA
A <-> AABBA
A <-> BBAAA
A <-> BBAAA <- (A, B) edge pairs contain two A's, so end of edge
A <-> AAAAA
Its also important to check for edge pairs that have swapped, see the following example
Checking edges for plot B
Checking third pair of rows
AAAAAA
AAABBA
AAABBA
^^^^^^
||||||
vvvvvv
ABBAAA
ABBAAA
AAAAAA
AAAAAA
AAABBA
AAABBA
| <- (A, A) edge contains no B's, so no edge found
ABBAAA
ABBAAA
AAAAAA
AAAAAA
AAABBA
AAABBA
| <- (A, B) edge contains one B, edge found!
ABBAAA
ABBAAA
AAAAAA
AAAAAA
AAABBA
AAABBA
| <- (A, B) edge contains one B, but so did
ABBAAA previous edge pair, so no new edge found
ABBAAA
AAAAAA
AAAAAA
AAABBA
AAABBA
| <- (B, A) edge contains one B, so did
ABBAAA previous edge pair, but plot id's
ABBAAA swapped, so new edge found!
AAAAAA
...
Continuing this for each plot, and each pair of columns and pair of rows, will give us the total number of edges for each plot.
One last caveat is the edges on the border of the grid (since we need to compare a row/column with nothing). This can be solved with some basic logic or by adding a border around the grid.
Day 13
Puzzle · SolutionPart 1
Today's puzzle can be represented as the following two equations:
$$ (a_x \times A) + (b_x \times B) = p_x $$ $$ (a_y \times A) + (b_y \times B) = p_y $$
Where ax, ay, bx, by are the accumulators for pushing the a and b buttons, px, py are the coordinates of the prize, and A, B are the number of times to push the A and B buttons.
We can solve this part using brute force, by starting at the highest value of B possible (min(px//bx, py//by, 100)), testing A from 0 to inf until either the equations match or go past the prize coordinates. If you overshoot without satisfying the equation, then decrement B until it reaches 0, at that point no solution is found.
But there is a more general way to solve this part, using a SAT solver such as Python's Z3. Here we can define the two equations above, and the two unknowns (A and B), and then solve. The following function defines the constraints and solves for A and B
from z3 import Solver, Int, sat
def solve(ax, ay, bx, by, px, py):
a_pushes = Int('a_pushes')
b_pushes = Int('b_pushes')
solver = Solver()
eq1 = (ax * a_pushes) + (bx * b_pushes) == px
eq2 = (ay * a_pushes) + (by * b_pushes) == py
solver.add(eq1, eq2)
if solver.check() == sat:
solution = solver.model()
return solution[a_pushes].as_long(), solution[b_pushes].as_long()
return 0, 0
Part 2
In part 2, the prize coordinates are too large to be solved via the brute force method described above. However, our general solution using a SAT solver can be directly applied here by just adding 10000000000000 to the x and y coordinates of the prize.
Solution via Linear Algebra
Both parts of this puzzle can also be solved using linear algebra. We can represent the problem equations above into a matrix representation:
$$ \begin{bmatrix} a_x & b_x \\ a_y & b_y \end{bmatrix} \begin{bmatrix} A \\ B \end{bmatrix} = \begin{bmatrix} p_x \\ p_y \end{bmatrix} $$
Solving for X
$$ \mathbf{M} \mathbf{X} = \mathbf{P} $$ $$ \mathbf{X} = \mathbf{M}^{-1} \mathbf{P} $$
Where the inverse of M is:
$$ \mathbf{M}^{-1} = \frac{1}{\text{det}(\mathbf{M})} \begin{bmatrix} b_y & -b_x \\ -a_y & a_x \end{bmatrix} $$
And the determinant of M is:
$$ \text{det}(\mathbf{M}) = a_x b_y - a_y b_x $$
Putting it all together:
$$ \mathbf{X} = \begin{bmatrix} A \\ B \end{bmatrix} = \frac{1}{\text{det}(\mathbf{M})} \begin{bmatrix} b_y & -b_x \\ -a_y & a_x \end{bmatrix} \begin{bmatrix} p_x \\ p_y \end{bmatrix} $$
This can then be broken down into the following two non-matrix equations
$$ A = \frac{(b_y p_x - b_x p_y)}{\text{det}(\mathbf{M})} $$
$$ B = \frac{(a_x p_y - a_y p_x)}{\text{det}(\mathbf{M})} $$
A solution is valid if both A and B are whole integer values. Putting the above into a function produces:
def solve(ax, ay, bx, by, px, py):
det = ax*by - ay*bx
A = (by*px - bx*py) / det
B = (ax*py - ay*px) / det
if int(A) == A and int(B) == B:
return int(A), int(B)
else:
return 0, 0
Day 14
Puzzle · SolutionPart 1
We can keep track of robots using their coordinates and for each time step increment their coordinates using the velocity values. In order to ensure that the coordinates don't go out of range we can use the modulo operator to wrap the value back around to the beginning. So after incrementing in the x axis, we modulo the value with the width. After incrementing in the y axis, we modulo the value with the height.
Counting the number of robots in each quadrant requires a few conditional statements to see if the coordinates go above or below the center x-axis and y-axis lines.
Part 2
Without knowing how the tree looks, the best initial solution is to print out the grid for each time step and use our visual cortex to find a tree shaped pattern. Doing so we eventually find a sub-grid containing a tree:
###############################
#.............................#
#.............................#
#.............................#
#.............................#
#..............#..............#
#.............###.............#
#............#####............#
#...........#######...........#
#..........#########..........#
#............#####............#
#...........#######...........#
#..........#########..........#
#.........###########.........#
#........#############........#
#..........#########..........#
#.........###########.........#
#........#############........#
#.......###############.......#
#......#################......#
#........#############........#
#.......###############.......#
#......#################......#
#.....###################.....#
#....#####################....#
#.............###.............#
#.............###.............#
#.............###.............#
#.............................#
#.............................#
#.............................#
#.............................#
###############################
In order to search for this tree programmatically, we can check for coordinates that form a continuous horizontal line. Specifically a line that spans 31 robots in width.
We can do this by grouping each column coordinate into rows. Then for each row, we sort the column coordinates, then iterate over the list, if two adjacent coordinates in the list are 1 space apart in coordinate space, then we increment a count value, otherwise we reset the count value. If the count value reaches 31 then we have found our horizontal line and thus our christmas tree.
Day 15
Puzzle · SolutionPart 1
Implementing the logic for most of the movement is pretty simple. If the next position for the robot to move is a . then move, if its a # then don't. Things get more difficult if we encounter a box (O). In order to move boxes we can check the next position past the box, if its empty (.) then we move the box and allow the robot to move. If the next position is another box then we check the position past that, here we need to keep track of which boxes will be removed from the grid and where they will end up (if they can move). If we ever encounter a wall tile, then we don't move anything, including the robot.
Part 2
The logic gets a bit messy for part 2 (at least for my solution). Expanding the grid is simple using Python's translation function on strings. But now we need to keep track of a pair of tiles representing each box.
The movement of the robot when not interacting with the box is the same, however if we need to move a box then three different paths of logic were implemented, moving: left, right, up/down. Note that in this implementation the position of the box is always the left tile of the box.
Moving Left
If a box is being pushed left, then we take the position of the robot as subtract two from the x-axis, this takes us to the left tile of the box. We can then check the next tile to the left, most of the logic in part 1 applies here, unless we are next to another box. If another box is on the left then we mark the current box to be removed, mark the tile on the left to add the box back in, and check the tile of the next box. However, instead of moving one tile left, we move two to account for the width of the box.
Moving Right
Moving right is similar to moving left. However, we need to increment the coordinates of the tile we are checking differently since we are approaching boxes from a different side.
Moving Up/Down
Moving up or down is more difficult since the original box can have a knock-on effect, moving various boxes that aren't directly above the original. Here we can implement logic to check the tiles above the left and right side of the box. If both tiles are . then we can move the boxes, if either above tile is a # then nothing moves. If a box is above either/both of the tiles then we need to move them.
To move boxes up and down we implement similar logic to left/right. However, instead of moving from one box to another linearly, there is a possibility that boxes branch, where one box moves two at a time. To resolve this, we can store the boxes that need checking in a queue. Whilst the queue is not empty (or until we reach a # tile), we pop from the queue and perform the logical checks described above, continuously keeping track of which boxes need moving (their original and new position).
A key point as mentioned earlier, is to always keep track of boxes from their left tile, in order to create some consistency in the code and reduce possible logical errors.
Day 16
Puzzle · SolutionPart 1
Part 1 can be solved using Dijkstra's algorithm. When getting the neighbours of the current cell, we need to keep track of which direction the neighbour is in and whether that is the same direction as the current cell. If the direction is different then we need to add 1000 to the distance of that neighbour.
Part 2
To solve part 2 we can use a modified depth first search to search all paths from the start to the end. We will modify the algorithm by allowing visiting the same node more than once, but to avoid getting stuck in loops, we will terminate a branch if it exceeds the optimal distance (the answer from part 1). For every node added to the stack, we will also keep track of all the nodes that led to that current node for that current branch/path. Every time we reach the end node, we store the path for returning later. Once we have exhausted all paths we count all the unique nodes from all the shortest paths found to get the answer to part 2.
The solution above works but is pretty slow since we are exploring all possible paths in the grid with a max distance of part 1 answer. To optimise this solution we can leverage more information gained from part 1 to prune the search space.
Dijkstra's algorithm stores the optimal path between the start and all nodes of interest leading to the end. Thus for every node being explored in our DFS, we can check if the distance exceeds what we know to be the optimal distance for that node. Since if the distance is higher, we know that the current path will never be able to reach the end in the shortest distance required.
Day 17
Puzzle · SolutionPart 1
Part 1 is fairly simple, we just need to implement the CPU and run the program. This can be broken down into two functions: step and get_combo which runs a single instruction and gets the combo oprand respectively. We can continue to step through the program until we reach a termination state (where the pointer goes out of bounds for either the opcode or oprand).
Part 2
Part 2 gets a bit more tricky. Brute forcing the problem will get us nowhere due to how large the A register will need to be. To solve this part we first need to reverse engineer the program. The following is the decompiled code for my puzzle input (yours will be almost the same with some value changes and a few instructions being swapped around).
_start:
bst A, 8
bxl B, 3
cdv A, B
bxc B, C
bxl B, 3
adv A, B
out B, 8
jnz 0
Note that the above has realised the combo oprands. First we can note that, for as long as register A isn't empty, the program will execute all the instructions then loop back to the start. So for each loop in the program, we can further break down the operations that are happening:
B = A % 8
B = B ^ 3
C = A >> B
B = B ^ C
B = B ^ 3
A = A >> 3
out = B % 8
Lets break this down step-by-step.
The first operation, gets the modulo of 8 (1000) which as explained in the puzzle description, truncates the A register to the lowest 3 bits. So the first step of the program is to get the 3 lowest bits from A and store them in B.
B = A % 8
The next couple of instructions ultimately will modify the B register.
B = B ^ 3
C = A >> B
B = B ^ C
B = B ^ 3
Next we bit-shift A by 3, essentially removing the last 3 bits from the A register
A = A >> 3
Finally, we output the last 3 bits of B
out = B % 8
Looking at all this then, we can determine a few things:
- The program loops until
Ais empty - The output of each loop is entirely dependant on the value of
A - Each loop mainly operates on the last 3 bits of
A(With the exception of theCregister - After each loop, the last 3 bits of
Aare removed
So essentially, the A register can be broken down into chunks of 3 (mostly) independent bits. With this and the information that each loop generates a single output, we can calculate how many bits are required to generate an output the length of our program.
The input program is 16 3-bit numbers long. And each 3-bit chunk of A generates a single output. So we will need to have 16 * 3 = 48 bits in our input to start generating outputs that are the same length as our program. That means there are 281474976710656 (2^48) possible combinations to search through.
Instead of searching through each combination, we can search through blocks of 3-bits at a time. This works since each output depends on a chunk of 3-bits. If we simulate the program with any value of A, we can observe that the last 3 bits of A are used to generate the first value of the output:
1 2 3 4 5 6
111 111 111 111 111 111
out = [6, 5, 4, 3, 2, 1]
So then, to solve this puzzle, we will apply the backtracking algorithm. Starting with the first 8 combinations of 3-bit numbers (0-7), running the program, and checking if any of the values generate the last value of the program.
Every time we find a value of A that generates a value equal to our program, we will set that 3-bit number in place and begin searching the next 3-bit block. If we find that after searching all 8 combinations of 3-bit numbers doesn't yield the expected output, then we backtrack to the last block of 3-bit numbers and continue our search. The code to do this can be seen below:
# generate the first 8 3-bit numbers
stack = [(a, 0) for a in range(8-1, -1, -1)]
while stack:
A, idx = stack.pop()
# run program on the current A value
output = run(program, A)
# if the output is smaller than expected or
# doesn't match the same value as the program
# for the current index, then skip
if (idx >= len(output)) or (output[-(idx+1)] != program[-(idx+1)]):
continue
# if the current index just checked was at the end of the program,
# than the entire program has been generated! return A
if idx == len(program) - 1:
return A
# current value of A is good, but we haven't generated all values yet
# so now generate the next 8 3-bit numbers and append them
# to the current chunks of 3-bit values tested
for next_A in range(8-1, -1, -1):
num = f'{A:03b}{next_A:03b}'
stack.append( (int(num, 2), idx + 1) )
Day 18
Puzzle · SolutionPart 1
Part 1 of this problem can be solved fairly easily using Dijkstra's algorithm, starting from the top corner (0,0) to the bottom corner (70,70). Where each movement adds 1 to the distance score and the location of the first 1024 bytes (#) are avoided.
Part 2
Since there aren't too many total bytes and we know that the first 1024 bytes create a valid path. We can simply brute force the solution to get our answer. This is done by incrementally adding a byte location to the grid, and running Dijkstra's algorithm to try and find a valid path. If no path is found then we return the coordinates of the byte.
Day 19
Puzzle · SolutionPart 1
We can check for valid towel designs by using the backtracking algorithm. For each pattern, we check if that pattern matches the beginning of the towel, if it does then we remove the first len(pattern) characters from the towel and start again. We continue this until we either have no characters left to check (in which case its valid) or none of the patterns match with the current beginning of the towel string, in which case we backtrack to before the last prefix truncation. We continue this until we either find a valid pattern combination or exhaust all possibilities. Consider the following example:
r, wr, b, g, bwu, rb, gb, br
bwurb
Performing our backtracking algorithm:
r, wr, b, g, bwu, rb, gb, br
bwurb
--
(r), wr, b, g, bwu, rb, gb, br
(b)wurb == r? No, checking next pattern
r, (wr), b, g, bwu, rb, gb, br
(bw)urb == wr? No, checking next pattern
r, wr, (b), g, bwu, rb, gb, br
(b)wurb == b? Yes, truncating and starting over
(r), wr, b, g, bwu, rb, gb, br
(w)urb == r? No, checking next pattern
...
(no valid patterns found for current sub-string, backtracking...)
...
r, wr, b, (g), bwu, rb, gb, br
(b)wurb == g? No, checking next pattern
r, wr, b, g, (bwu), rb, gb, br
(bwu)rb == bwu? Yes, truncating and starting over
...
r, wr, b, g, bwu, (rb), gb, br
(rb) == rb? Yes, truncating leaves string empty, valid combination found!
Below is code implementing this using recursion:
def valid(towel, patterns):
if len(towel) == 0:
return True
for p in patterns:
if towel.startswith(p):
if valid(towel[len(p):], patterns):
return True
return False
Part 2
For part 2, we can modify our above function to, instead of returning with the first combination found, keep a count of all combinations found and return the total. That is done with the below code:
def count(towel, patterns):
if len(towel) == 0:
return 1
total = 0
for p in patterns:
if towel.startswith(p):
total += count(towel[len(p):], patterns)
return total
Whilst the above function works, it will have to check a whole lot of combinations before returning the final answer. To speed this up, we can leverage the fact that once a sub-string has been processed and number of combinations returned, we don't need to process it again. So we can use memoization to store the total number of combinations for a given sub-string. If the total has already been computed then we return that instead of computing it again. Below is the same function with added memoization:
def count(towel, patterns, mem):
if len(towel) == 0:
return 1
if towel in mem:
return mem[towel]
total = 0
for p in patterns:
if towel.startswith(p):
total += count(towel[len(p):], patterns, mem)
mem[towel] = total
return total
Day 20
Puzzle · SolutionPart 1
This puzzle can be solved by recognising that if there were no walls then the shortest distance between any two points is just the Manhattan distance. So we first need to get the original path using Breadth-first search. Then for every pair of points (a, b) on the path, compute the Manhattan distance between them, if the distance is less than 2 (the number of picoseconds you can phase through walls) then given the cheating constraints, you could get from point a to point b in distance picoseconds. We then need to subtract the normal number of picoseconds it would take to get from point a to point b with the new cheated time to get the time saved between those points. We simply increment a counter for all pair of points producing at least 100 picoseconds of time saved.
Which walls we phase through doesn't need to be known directly but can easily be implied since a cheating time of 2 picoseconds only allows us to connect two point with a single wall # between them.
Part 2
We can adapt our solution to day 1 to give us the answer to part 2 by simply computing the time saved between all pairs of points on the original path that have a Manhattan distance of at most 20 (compared to at most 2 in part 1). This simple modification is all that's required to solve part 2!
The code for both paths can be seen below (BFS is just a general breadth-first search implementation):
def solve(x):
grid = aoc.Grid(x)
s = grid.find('S')[0]
e = grid.find('E')[0]
path = BFS(grid, s, e)
p1, p2 = 0, 0
for i in range(len(path)-1):
for j in range(i+1, len(path)):
d = grid.dist(path[i], path[j])
if d <= 2:
p1 += int(((j-i)-d) >= 100)
if d <= 20:
p2 += int(((j-i)-d) >= 100)
return p1, p2
Day 21
Puzzle · SolutionPart 1
This problem can be broken down by recognising that we need to find optimal paths between each pair of buttons. We can then iterate over the sequences of button presses and expand out each button pair into its respective optimal path.
The shortest path between any two points can be found using Breadth-first search, where we ensure we don't go over the blank space.
For some button pairs, there are various paths of the same length. However, not all paths are created equal. Lets investigate a path for a pair of buttons on the first robot's keypad. The keypad can be seen below:
+---+---+
| ^ | A |
+---+---+---+
| < | v | > |
+---+---+---+
Lets investigate the paths for the button pair >^. There are two paths with the same optimal distance:
<^A
^<A
We know they both have the same distance as we can check the Manhattan distance between each pair of buttons:
<^A
<^ = 2
^A = 1
^<A
^< = 2
<A = 1
So far it all looks even! However, lets keep going an trace some paths that the second robot will have to execute to push the above button sequence. We will prepend an A to the sequence, since the second robot will have to start there.
A<^A
A< <^ ^A
Av<<A, A>^A", A>A"
A^<A
A^ ^< <A
A<<A, Avv<<A, A>>>>^^A
Now lets compute the Manhattan distances for each pair in each sequence and sum them together to get the total cost of each option:
A<^A
A< <^ ^A
Av, v<, <<, <A A>, >^, ^A A>, >A
3 2 1 4 2 3 2 2 2 = 21
A^<A
A^ ^< <A
A<, <A Av, v<, <A A>, >>, >^, ^A
4 4 3 2 4 2 1 4 21 = 26
As we can see, when taking into account the second robot, now the first path (<^A) is more optimal!
Given all of this then, its not enough to find one path using BFS. Instead, we can apply some brute force and search all possible combinations of optimal paths between two pairs of buttons. The final second-robot button sequence that has the shortest length can then be used to compute the answer to part 1.
Part 2
We could apply the same solution above to part 2, but with a robot depth of 25. However, looking at the input, we can see that it seems to be growing quite large, and for each level of depth we go, we will have to branch more and more to find the most optimal path. Lets do some back of the envelope math.
The original sequence is 5 buttons long if we include starting at A. This produces 4 pairs of buttons we need to traverse. Lets be optimistic and assume that each level of button sequences only requires one branch (so one pair of buttons have 2 possible optimal solutions). With this doubling factor each time, we end up with 33,554,432 branches to check. Considering this is an optimistic estimate, we can assume much worse. Thus we need to improve this solution.
The first improvement is to recognise that there are at most 11^2 + 5^2 = 146 button pairs. So if we can figure out all the optimal paths for each button pair, we can store them in a dictionary. Then for each sequence of button presses, we can decompose it into button pairs (start, end), and use our map to determine the best sequence, instead of calculating it every time with BFS. Note: I won't go into how to calculate the optimal paths since I did it manually with some trial and error.
However, we have another problem, the final sequence of button presses is going to be quite long. Assume the number of button presses double every time. We will end up with around 4^25 = 1,125,899,906,842,624 buttons in the sequence.
Instead of storing this then, we can store, for each button sequence, how many times each pair of buttons appear. So for the sequence <A^A>^^AvvvA, we would have:
A^ = 1
^A = 2
A> = 1
>^ = 1
^^ = 1
Av = 1
vv = 1
vA = 1
This way, our Counter only has to store at most 146 keys (as calculated earlier).
Using both of these optimisations, we can solve part 2 in a few milliseconds!
Day 22
Puzzle · SolutionPart 1
Part 1 just requires implementing the logic to evolve each secret in the input. Perform this evolution process 2000 times and sum to get the answer.
Part 2
For part 2, we need to keep track of both the last digit of each secret, but also the changes between each number. For each number in the input, we evolve the secret, then compute and store both the last digit of the secret and the difference between it and the previous digit.
Using this sequence of changes and digits, we can then run a sliding window of length n=4 over each sequence. For each n=4 window, we'll update a global counter with the window as the key and the sum of all digits associated with that window for each sequence. Once we have iterated over all the sequences of changes, we will have a counter that has all possible n=4 windows and the sum of all the respective digits for that window found in the all the sequences. Getting the largest sum from this counter will give us the answer!
Note that, for each sequence, we should only update the counter once for each window found, even if that window occurs again in the sequence with a higher digit.
Day 23
Puzzle · SolutionPart 1
This puzzle involves a undirected graph, and for part 1 we are looking for triangles in the graph. Which are 3 nodes connected to each other. We can do this naively by iterating over each node n in the graph, then for each connected node nn , iterate over each node connected to nn (nnn). If nnn is also connected to n then add the triangle to a list. Since the input graph is small enough this solution will work fine. One thing to note is that this solution will have duplicates (e.g. a, b, c and b, c, a and ...). To remove these we can just sort each tuple of nodes and make the list into a set.
The graph for the example input can be seen below. Edges that belong to a triangle are highlighted in red.
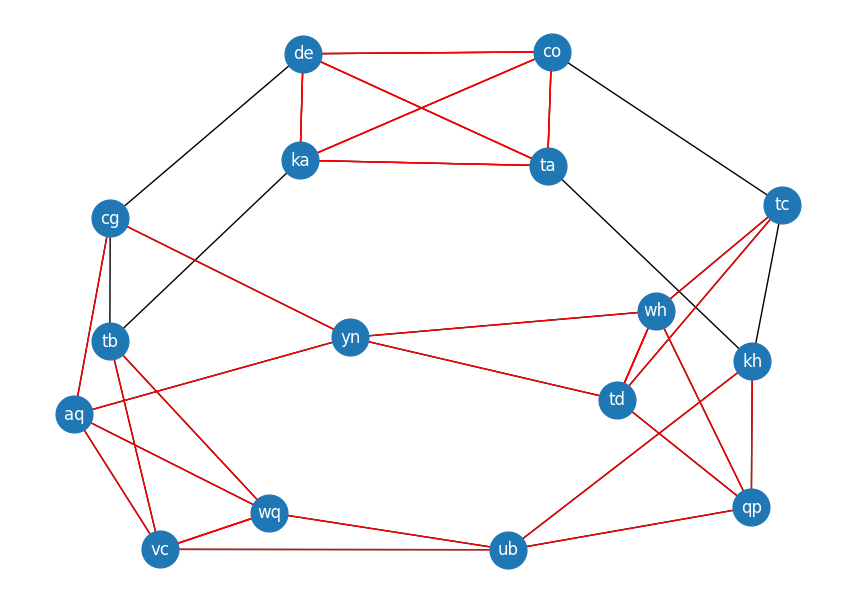
Part 2
For part 2 we are trying to find cliques, which are sub-graphs where all nodes are connected to each other (triangles are just cliques containing 3 nodes). Specifically, we are trying to find maximal cliques, which are cliques that are not apart of larger cliques. For example if the nodes a, b, c, d where all connected to each other, forming a clique. Then the nodes a, b, c would also be a clique, but not a maximal one.
Brute forcing the solution like in part 1 is going to be too slow. So instead we can use the Bron-Kerbosch algoritm to find all maximal cliques. Then out of all maximal cliques, we can get the one with the most nodes. The pseudocode for Bron-Kerbosch algorithm can be seen below:
R = current clique
P = candidate vertices to be added to R
X = set of vertices already processed
algorithm BronKerbosch(R, P, X) is
if P and X are both empty then
report R as a maximal clique
for each vertex v in P do
BronKerbosch(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}
The python code to implement this is below, where graph is a dictionary, where the keys are vertices, and the values are the set of all connected vertices to the key.
def bron_kerbosch(r, p, x, graph):
maximal_cliques = []
if not p and not x:
maximal_cliques.append(r)
for v in list(p):
maximal_cliques.extend(
bron_kerbosch(r | {v}, p & graph[v], x & graph[v], graph)
)
p.remove(v)
x.add(v)
return maximal_cliques
The above function will return all maximal cliques. We then need to find the largest one, sort the vertices, and print them to get the answer.
Intuition behind the Bron-Kerbosch algoritm
In the algorithm, we are recursively iterating over each node in the graph and assuming it belongs to a clique. We add the node to R (our current hypothesised clique), as well as keeping track of the candidate nodes (previous candidates union adjacent nodes), and the nodes already seen (previous seen nodes union adjacent nodes)
If P is empty, that means there are no more vertices left to explore (out of all the adjacent nodes in our hypothesised clique). If X is empty that means there were no vertices left over.
For a given vertex v if we have checked all adjacent vertices then P will be empty. If X is not empty however, then that means there are nodes left over that weren't connected to all the nodes in the sub-graph.
This is because we check every node in the sub-graph via the for loop, and every time we remove that vertex from X, so if X isn't empty there are vertices that aren't apart of the sub-graph. We know which nodes are apart of the sub-graph because for any given vertex v we only check adjacent vertices P that have both (already been found in a previous vertex) and (is an adjacent vertex for the current vertex v).
Day 24
Puzzle · SolutionPart 1
Part 1 is pretty simple. First we store all of the values in a dictionary, then store all of the instructions in a queue. Then iterate over each instruction (popping left from the queue) and if the output value doesn't exist yet then append it back into the queue and move on to the next instruction.
Part 2
Part 2 is more difficult, there are far too many values to iterate over all possible combinations of swaps. Instead we can visualise the operations to try and try to make sense of the circuit:

The original image is quite large and thus slow to load. For the full size image, click here
Here the inputs nodes and output nodes have been horizontally aligned. We can see that most of the operations flow straight down, and have a bunch of operations flowing diagonally from the top right to the bottom left.
The puzzle helps us out by telling us that this circuit is meant to be implementing an adder. We can assume that the above diagram is implementing a regular full-adder circuit. A normal cull-adder circuit can be seen below:
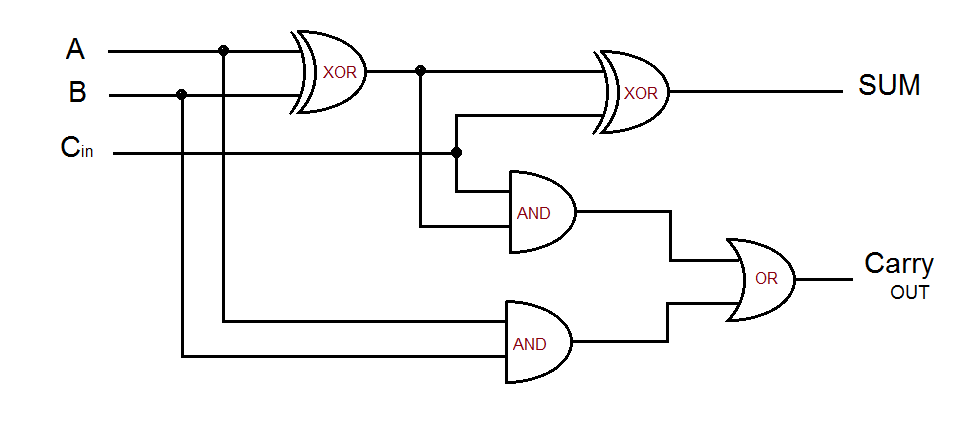
Here the adder circuit takes in three inputs a, b, c, where c is the carry bit (overflow from the previous binary addition, if both a and b are 1). Essentially then, our circuit is comprised of various adder modules that are only connected to each other via a single carry line, much like a normal binary adding circuit. We can see one of the adder modules if we zoom in on our graph:
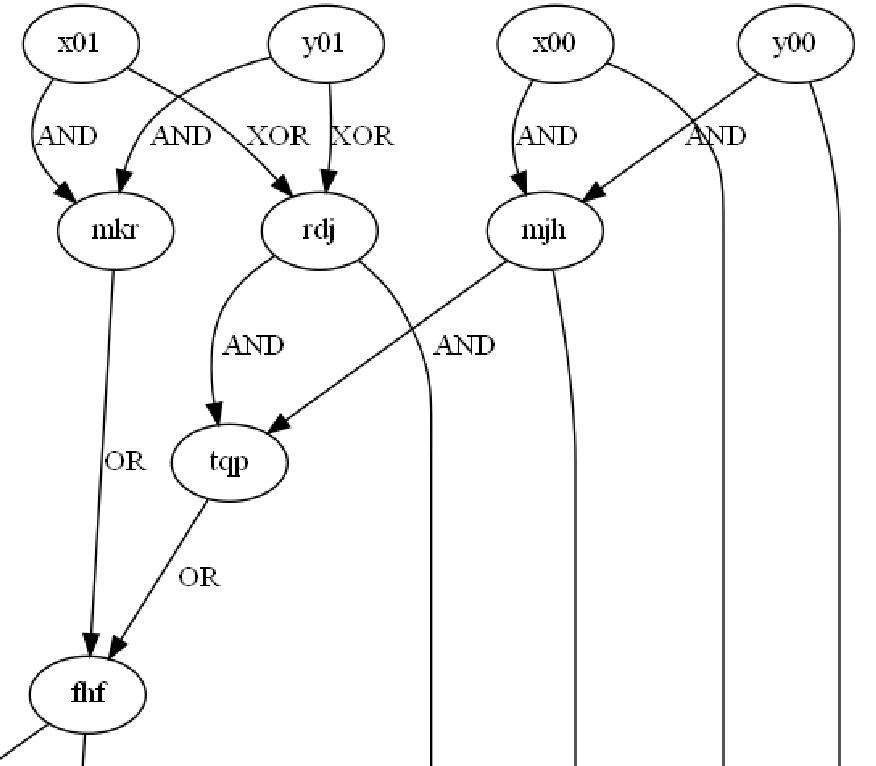
Here x01 = a, y01 = b, and mjh = c. The final XOR operation is at the bottom of the graph and hence not visible, however the output of rdj and mjh feed into what would be z01. fhf then goes on to be the carry bit for the next adder circuit.
Using this knowledge then, we can visually inspect the graph for things that don't look right. Starting at all of the output nodes (nodes starting with a z), we know they should always be an XOR operation. However, for my input there are 3 output nodes that are made with either an AND or an OR operation. Luckily, the two values that need to be swapped are always apart of the same adder module, so a quick inspection reveals an value with an XOR operation where there should be either a AND or OR. Hence, this is the value that needs to be swapped with our corrupted output value.
The last pair of corrupted values for my input existed at the top of the graph. The tool used to render this graph has helpfully displayed all AND operations at the top, right below the inputs. However, for one value we can see an XOR instead. Inspecting that module reveals another value with an AND operation where there should be an XOR.

Taking all of these values then, we can sanity check ourselves by swapping the values, then running the same code as part 1. We then simply sort the values that have been swapped and output them as a comma separated string to give us the answer to part 2.
Day 25
Puzzle · SolutionPart 1
Today's puzzle can be solved by first separating the grids into locks and keys. This can be done by checking the top left tile, if its a # symbol then the grid is a lock, otherwise its a key. Next, for each grid, we separate it into columns and count the number of # symbols and subtract by one, this gives us the pin heights for the locks and keys. Then for each pair of lock and key, we compare the pin heights. If any pair of pin heights summed together are greater than 5, then the pairing is invalid. If none of the summed pair of heights are greater than 5, then the pairing is valid.
Part 2
As per usual, there is no part 2 for the last day so that's all for this years Advent of Code.
Merry Christmas everybody!